153ZODH / 9. cvičení: Porovnání verzí
→Osnova: teorie |
m →Teorie: fft |
||
| Řádek 18: | Řádek 18: | ||
Tuto metodu lze využít např. pro identifikaci a eliminaci periodického šumu obsaženého v družicovém snímku. V tomto případě je nejprve provedena Fourierova transformace, posléze aplikována maska (šum se zobrazí ve Fourierově spektru ve tvaru pruhů) a data zpětně transformována do prostorové domény (inverzní Fourierova transformace). | Tuto metodu lze využít např. pro identifikaci a eliminaci periodického šumu obsaženého v družicovém snímku. V tomto případě je nejprve provedena Fourierova transformace, posléze aplikována maska (šum se zobrazí ve Fourierově spektru ve tvaru pruhů) a data zpětně transformována do prostorové domény (inverzní Fourierova transformace). | ||
== FFT == | |||
Aplikace Fourierovy transformace (Fourierova transformace v diskrétním tvaru - ''Fast Fourier Transformation'' - FFT): | |||
# nastavit výpočetní region | |||
# | |||
g.region rast=tm1 | |||
# | |||
# Fourierova transformace | |||
# | |||
i.fft input=tm1 real=tm1_r imag=tm1_i | |||
Následně můžeme vrstvy (reálnou 'tm_r' a imaginární část 'tm_i') vzniklé po Fourierově transformaci zobrazit v GRASS monitoru: | |||
# nastavit region a zobrazit výsledné obrazové vrstvy | |||
# | |||
g.region rast=tm1_r | |||
d.erase -e | |||
d.rast tm1_r | |||
d.rast tm1_i | |||
[[Soubor:ZOD-cv8-tm1_r.png|frame|center|Obr č.2: Reálná část Fourierova spektra]] | |||
Verze z 28. 11. 2008, 22:45
< Stránky předmětu • Předchozí cvičení • Další cvičení
Osnova
Teorie
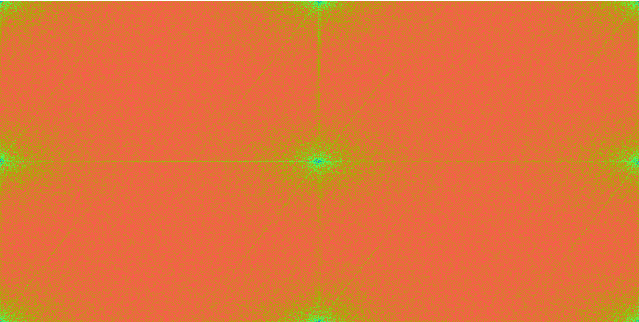
Fourierova transfomace je založena na převodu dat z geometrického znázornění (tj. prostorového souřadnicového systému) do domény frekvenční (souřadnicového systému frekvenčního) - komplexního znázornění složkových četností výskytu. Během této transformace je tak obraz rozložen na frekvenční komponenty (diskrétními DH je proložena spojitá funkce, jde o funkce sinus a kosinus s různými amplitudami, frekvencemi), které jsou uloženy jako komplexní čísla. V případě dvoudimenzionální Fourierovy transformace jsou výsledkem dvě obrazové vrstvy - reálná a imaginarní část.
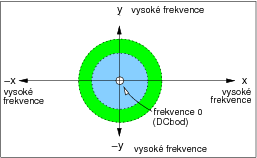
Tyto četnosti výskytu jsou rozloženy podél obou os a lze je znázornit ve dvourozměrném rozptylogramu (tzv. Fourierově spektru). Nulový bod ("DC" - direct current) má četnost 0,0 (viz obr. č.1). Se vzrůstající vzdáleností od nulového bodu stoupají četnosti výskytu (jsou kolem DC uspořádány symetricky). Jevy, které mají v původním obraze horizontální trend se vyskytují ve vertikálních komponentách Fourierova spektra a naopak.
Tuto metodu lze využít např. pro identifikaci a eliminaci periodického šumu obsaženého v družicovém snímku. V tomto případě je nejprve provedena Fourierova transformace, posléze aplikována maska (šum se zobrazí ve Fourierově spektru ve tvaru pruhů) a data zpětně transformována do prostorové domény (inverzní Fourierova transformace).
FFT
Aplikace Fourierovy transformace (Fourierova transformace v diskrétním tvaru - Fast Fourier Transformation - FFT):
# nastavit výpočetní region # g.region rast=tm1 # # Fourierova transformace # i.fft input=tm1 real=tm1_r imag=tm1_i
Následně můžeme vrstvy (reálnou 'tm_r' a imaginární část 'tm_i') vzniklé po Fourierově transformaci zobrazit v GRASS monitoru:
# nastavit region a zobrazit výsledné obrazové vrstvy # g.region rast=tm1_r d.erase -e d.rast tm1_r d.rast tm1_i