Tento text se vztahuje k akademickému roku 2006/2007. Aktuální stránky cvičení jsou dostupné zde.

Filtrace obrazu, plovoucí okno, vyhlazování obrazu

osnona

V tomto kurzu si představíme další metodu zpracování digitálního obrazu a to filtraci. Jde o stěžejní metodu zvýraznění obrazu používanou při řešení rozmanitých úloh. Uvedeme základní typy filtrů a jejich možné použití. Přirozeně se budeme soustředit na možnosti filtrování obrazu v GISu GRASS.

seznam příkazů

filtrace obrazu

Filtrací obrazu rozumíme v obecné rovině operace s digitálním obrazem, které slouží ke zvýraznění určité informace. Rozlišujeme celou řadu metod filtrace obrazu od velmi jednoduchých (např. prosté průměrování) až po poměrně komplexní, sofistikované metody.

Filtrace může být využívána pro vyhlazení obrazu, potlačení šumu, zvýraznění kontrastu, detekci hran, postklasifikační zpracování obrazu a řadu dalších úloh. Vzhledem k rozsahu většiny digitálních dat je z technického hlediska nevhodné řešit podobné úlohy najednou v celém obrazu. Daný filtr je tak definován jako šablona rastrové matice (tzv. "moving window", v české literatuře se často využívá termín "kernel") - tedy pohybujícího se (plovoucího) okna. Jde o matici (většinou čtvercovou) tvořenou lichým počtem řádků a sloupců, která se při výpočtu pohybuje nad maticí originálních dat (ve směru řádků a sloupců). Nová hodnota rastrové buňky je určena na základě aritmetické operace či statistické veličiny definované filtrem a hodnot originálních dat. Do výpočtu tak vstupuje na rozdíl například od podílu obrazu množina hodnot a nikoliv pouze jedna jediná hodnota. Jde tedy o lokální a nikoliv bodové operace. Nejčastěji se využívá velikost kernelu 3x3 a 5x5.

Filtry lze rozdělit na dva základní typy:

filtry s nízkou (low pass) propustností, které ořezávají vysoké frekvence (dochází tak k potlačení výraznějších detailů (např. liniových prvků) a současně zdůraznění jevů s malými změnami)
- omezují odchylky od lokálního průměru
- vyhlazuje detaily původního obrazu
- redukují rozsah stupňů šedi
filtry s vysokou (high pass) propustností, které naopak zdůrazňují vysoké frekvence (to znamená zdůraznění výraznějších detailů a současné potlačení jevů s malými změnami). Jde především o ostřící filtry a hranové operátory.
- zvětšují detaily v ploše snímku

možnosti filtrování obrazu v GRASSu

Pro definování maticového filtru mohou být ve své podstatě použity dva moduly GRASSu - r.mapcalc a r.mfilter. První uvedený modul nabízí maximální flexibitu - umožňuje uživateli definovat v podstatě libovolný filtr (šablonu kernelu). Na druhou stranu je méně "přivětivý" - definice filtru je poněkud zdlouhavější. Použití modulu r.mfilter je naopak velmi jednoduché, umožňuje velmi snadnou definici filtru a jeho následnou aplikaci. To je vykoupeno poněkud omezenými možnostmi - např. neumožňuje definovat kernel obsahující realná čísla. Tento modul se tedy hodí pro nepříliš komplikované filtry, naopak r.mapcalc je v podstatě jedinou volbou v případě komplikovanější podoby kernelu (šablony matice filtru). My si prakticky vyzkoušíme oba výše zmíněné moduly.

prosté průměrování

Nová hodnota (zaokrouhlena na celé číslo) středového pixelu je vypočtena jako aritmetický průměr hodnot pixelů pokrytého kernelem. Ve svém důsledku tento filtr likviduje liniové elementy (jde o nízkofrekvenční filtr), naopak je vhodný pro vyhlazení výsledku klasifikace u rozsáhlejších homogenních ploch či pro částečné odstraňování šumu. Rovnice pro velikost kernelu 3x3:

$p(i,j)={\frac {1}{9}}\sum _{k=-1}^{1}\sum _{l=-1}^{1}f(i+k,j+l)$

Na tomto filtru si ukážeme jak postupovat při jeho definici - jak pomocí r.mfilter, tak r.mapcalc.

r.mfilter

Vytvoříme kernel o velikosti 3x3, jeho definici uložíme do zvláštního textového souboru (prumer3.txt):

TITLE   proste prumerovani (3x3)
MATRIX 3
1 1 1
1 1 1
1 1 1
DIVISOR 9
TYPE P

Popis formátu:

TITLE     - textový popisek fitru
MATRIX    - velikost kernelu, resp. matice (povolena pouze čtvercová matice, rozměr je liché číslo)
x y z ... - naplnění matice - konstanta, kterou bude přenásobena hodnota buňky originálních dat
. . .
DIVISOR   - dělitel
TYPE P|S  - typ filtru (paralelní nebo sekvenční)

Z tohoto pohledu tedy rozlišujeme dva základní typy filtrů:

sekvenční - pro výpočet nové hodnoty středové buňky využívá již modifikované hodnoty sousedních buněk
paralelní - pracuje pouze s hodnotami buněk originálních dat

Filtr aplikujeme pomocí r.mfilter takto:

#nutno nastavit požadovaný region!
#
GRASS~ > g.region rast=tm1
GRASS~ > r.mfilter in=tm1 out=tm1_p3 filter=prumer3.txt

Textový soubor může obsahovat definice i více filtrů najednou, které jsou posléze aplikovany v daném pořadí. Navíc lze pomocí parametru repeat docílit opakovaného aplikování daného filtru.

r.mapcalc

Šablona kernelu se při použití tohoto modulu definuje pomocí relativních souřadnic vztažených ke středovému pixelu matice. Tak například souřadnice [-1,-1] odkazuje na buňku ležící řádek nad centrální buňkou a jeden sloupec vlevo; podobně [0,2] odkazuje na buňku ležící ve stejném řádku jako buňka centrální a dva sloupce napravo.

Filtr prostého průměrování bude v zápisu pro r.mapcalc vypadat takto:

#filtr "prosté průměrování" pro r.mapcalc
#
GRASS~ > r.mapcalc 'tm1_p3_mc = (tm1[-1,-1]+tm1[-1,0]+tm1[-1,1]+\
tm1[0,-1]+tm1[0,0]+tm1[0,1]+\
tm1[1,-1]+tm1[1,0]+tm1[1,1])/9'

Výslednou obrazovou vrstvu můžeme zobrazit v GRASS monitoru:

#výchozí tabulku barev "rainbow" přenastavit na "grey.eq"
#
GRASS~ > r.colors tm1_p3 col=grey.eq

Obr č.1: Detail prvního kanálu LandSat-TM5: vlevo originální data, vpravo po aplikaci filtru "prostého průměrování" (kernel 3x3)

Pro názornější ilustraci uvedeme aplikaci filtru prostého průměrování (3x3 a 5x5) na uměle vytvořených testovacích datech, viz obr č.2 a č.3.

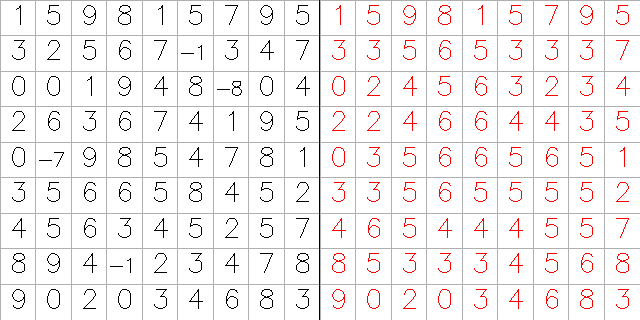
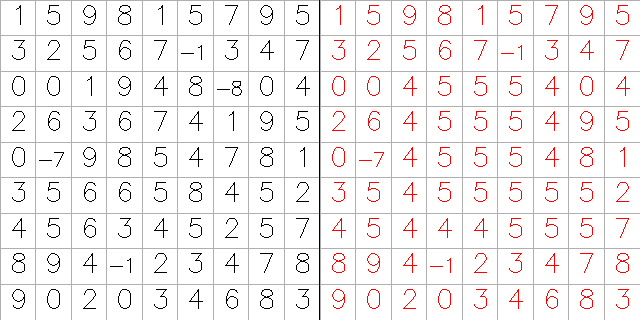
Obr č.2: Testovací data: vlevo originální data, vpravo po aplikaci filtru prostého průměrování, velikost kernelu 3x3

Obr č.3: Testovací data: vlevo originální data, vpravo po aplikaci filtru prostého průměrování, velikost kernelu 5x5

příklad filtru s nízkou a vysokou propustností

Na tomto místě si prakticky vyzkoušíme aplikaci low pass a high pass filtru.

filtr s nízkou propustností (low-pass.txt):

TITLE low pass (3x3)
MATRIX 3
1 1 1
1 1 1
1 1 1
DIVISOR 9
TYPE S

filtr s vysovou propustností (high-pass.txt):

TITLE high pass (5x5)
MATRIX 5
-1 -1 -1 -1 -1
-1 -1 -1 -1 -1
-1 -1 24 -1 -1
-1 -1 -1 -1 -1
-1 -1 -1 -1 -1
DIVISOR 25
TYPE S

Aplikaci filtrů provedene zcela analogiky:

GRASS~ > g.region rast=tm1
#
# low pass filtr
#
GRASS~ > r.mfilter input=tm1 output=tm1_lp filter=low-pass.txt
GRASS~ > r.colors map=tm1_lp color=grey.eq
#
# high pass filtr
#
GRASS~ > r.mfilter input=tm1 output=tm1_hp filter=high-pass.txt
GRASS~ > r.colors map=tm1_hp color=grey.eq

Vybereme-li vhodný detail, můžeme výsledky obou filtrů porovnat (viz obr č.4). Z obrázku je zřetelné, že filtr s nízkou propustností (low pass) skutečně potlačuje ostré přechody DH v datech (např. liniové struktury) a naopak filtr s vysokou propustností (high pass) tyto struktury zdůrazňuje.

Obr č.4: První kanál LandSat-TM5: originální data, data po aplikaci filtru s nízkou a vysokou propustností

operace v okolí

Na tomto místě bude představen další modul GRASSu - r.neighbors. Jde o modul, který pracuje na bázi dobře známého plovoucího okna (kernelu). Výsledná hodnota centrálního pixelu může být určena jako (viz parametr method):

average - průměrná hodnota
median - medián
mode - modus
minimum - minimální hodnota
maximum - maximální hodnota
stddev - směrodatná odchylka
sum - suma hodnot
variance - variance (rozptyl) hodnot
diversity - počet rozdílných hodnot v okolí
interspersion - počet hodnot (v procentech + 1) lišících se od hodnoty centrální buňky

Velikost kernelu určíme pomocí parametru size. Tak například filtr "prostého průměrování" vypadá v zápisu r.neighbors takto:

GRASS > r.neighbors input=tm1 out=tm1_p3_nb size=3 method=average

mediánová fitrace

Tato filtrace patří mezi nelineární filtrace obrazu. Nedochází k výpočtu střední hodnoty, ale určení mediánu (tj. prostředního členu uspořádané posloupnosti všech hodnot ze zvoleného okolí).

GRASS > r.neighbors input=tm1 out=tm1_med size=3 method=median

módová filtrace

Je vhodná pro čištění map po klasifikaci. Módus je nejčastěji se vyskytující hodnota.

GRASS > r.neighbors input=tm1 out=tm1_mod size=3 method=mode

Některé operace v okolí lze alternativně provést pomocí univerzálního modulu pro rastrovou algebru r.mapcalc (např. mediánová filtrace):

GRASS > r.mapcalc 'tm1_med_mc = median(tm1[-1,-1],tm1[-1,0],tm1[-1,1],\
tm1[0,-1],tm1[0,0],tm1[0,1],\
tm1[1,-1],tm1[1,0],tm1[1,1])'

Oba dva výše uvedené filtry patří mezi filtry s nízkou propustností.

Gaussův filtr

Jedná se o metodu, při které se pro jednotlivé pixely pokryté kernelem vypočtou váhové koeficienty podle Gaussovy funkce:

$G(i,j)=exp{\bigg (}{\frac {-[(i-u)^{2}+(j-v)^{2}]}{2\sigma ^{2}}}{\bigg )}$

Váhy V(i, j) se určí normalizací hodnot G(i, j):

$P(u,v)={\frac {1}{9}}\sum _{i=-1}^{1}\sum _{j=-1}^{1}V(i,j)p(i,j)$

Pro praktické použití můžeme využít již připravený filtr (autorem je Jáchym Čepický) - gaussian.pl. Jde opět o zástupce nízkofrekvečních filtrů.

# nutné nastavit příznak spustitelnosti souboru
#
$ chmod +x gaussian.pl
GRASS~ > ./gaussian.pl -t 2.5 -i tm1 -o tm1_gauss | r.mapcalc

Obr č.5: Detail prvního kanálu LandSat-TM5: vlevo originální data, vpravo po aplikaci Gaussova filtru

[ Zpracování obrazových dat ]